Собственное время, события и мировые линии частиц
В качестве часов наблюдатели в системах S, Sў могут использовать любой
периодический процесс, например, излучение атомов или молекул на определенных
фиксированных частотах. Время, отсчитываемое по часам, движущимся вмемте с
данным объектом, называется собственным временем этого объекта.
Для измерения длин можно взять некоторый эталон - линейку. Собственной
длиной линейки называется ее длина l0 в той системе, в которой она
покоится. Величина l0 равна модулю разности координат концов линейки в один
и тот же момент времени.
Совокупность декартовых координат 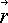 = (x,y,z) и момента времени
t в некоторой инерциальной системе отсчета определяют событие.
Событием является, например, нахождение точечной частицы в момент времени t
в точке пространства, указанной вектором = (x,y,z) и момента времени
t в некоторой инерциальной системе отсчета определяют событие.
Событием является, например, нахождение точечной частицы в момент времени t
в точке пространства, указанной вектором 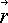 . .
Множество всех событий образуют "четырехмерный Мир Минковского". Отдельные
точки в четырехмерном пространстве указывают координаты и время некоторого
"события". Последовательность кинематических состояний любого тела (его
координаты в разные моменты времени) изображается мировой линией
(Рис. 7).
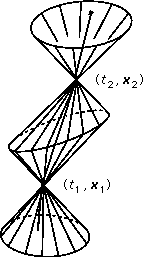 Рис. 7
Рис. 7
Если частицы движутся только вдоль оси 0x, то наглядно представить
"Мир Минковского" можно с помощью плоскости координат (с t, x). Время
удобно умножить на скорость света, чтобы обе координаты имели одинаковую
размерность. Это можно сделать, поскольку скорость света -
универсальная мировая константа.
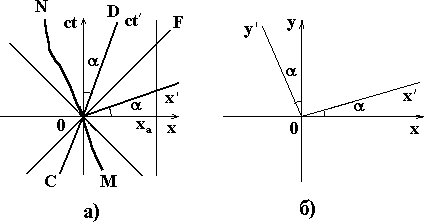
Рис. 8
Мировыми линиями (в отличие от траекторий классической механики) обладают не
только движущиеся, но и покоящиеся в данной инерциальной системе отсчета тела.
Так, мировая линия тела, покоящегося в начале координат, будет совпадать с
временной осью 0 ct, а тела, покоящегося в пространственной точке xa -
является прямой AB, параллельной оси времени. Мировая линия тела,
движущегося с постоянной скоростью V - (и при t = 0,
находящегося в точке x(0) = 0) - прямая CD; мировая линия светового луча,
испущенного из начала координат в напралении оси x - биссектриса
координатного угла OF;
мировая линия тела, движущегося с переменной скоростью v(t) - кривая MN
(cм. Рис. 8а))
|