Непривычные следствия СТО породили множество парадоксов. Один из них носит название "парадокса шеста и сарая":

Пусть шест длиной l₀ = 20м движется со скоростью 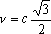. Расчет по формуле (11) показывает, что в системе неподвижного сарая его длина равна l = 10м. Тогда в некоторый момент времени он целиком помещается в сарае длиной L₀ = 10 м. Однако в системе "шест" длина сарая L₀ = 5 м. Как же может поместиться 20-ти метровый шест в 5-ти метровом сарае?

Такие "парадоксы", как правило, "выпячивают" одно из положений теории и обычно легко разрешаются, если вспомнить другие следствия СТО. В данной задаче рассматриваются четыре события, связанные с концевыми точками шеста (a₁, a₂) и линейки (n₁, n₂) - концы которой определяют границы сарая. По условию задачи события (a₁, n₁) и (a₂, n₂) - одновременны в системе сарая S, но в системе "шест" S^ў они не будут одновременны: (сначала острие копья достигает задней стенки сарая и только следом задний конец копья скроется в сарае). Поэтому поставленный вопрос не имеет смысла.